How high should you hang a mirror...?
by Bavi_H, 3/25/2008
When my sister hung my mirror too low, my head was cut off in the reflection. I made up the following problem in order to find the best height to hang a mirror, but wasn't able to solve it until recently.
How high should you hang a mirror so that the angles of the left over space above and below your reflection in the mirror are equal?
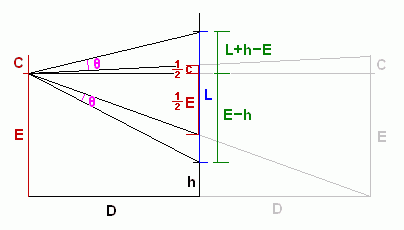
E is the height of your eyes.
C is the distance from your eyes to the top of your head. (C for crown.)
L is the length of the mirror.
D is the distance from you to the wall.
h is how high from the floor you should hang the mirror.
θ is the angle of the left over space above and below your reflection.
I was able to write an equation setting the angle of the left over space above the reflection equal to the angle of the left over space below the reflection:
But I didn't know how to proceed to solve for h. With some help from mathematicians at the Wikipedia Reference Desk and the automated solver at Quickmath I've finally found the solution.
Here's an example solution using values for my mirror and body measurements.
E = 69 inC = 4 in
L = 48 in
D = 36 in
h = 26.70075 in
θ = 5.818472°
Using the same values for E, C, and L, here are graphs that show how h and θ change as D increases.
Update
When I actually tested the results by positioning my mirror and looking at my reflection, I noticed that my feet were taking up room that I hadn't accounted for. Here's an updated solution.
How high should you hang a mirror so that the angles of the left over space above and below your reflection in the mirror are equal?
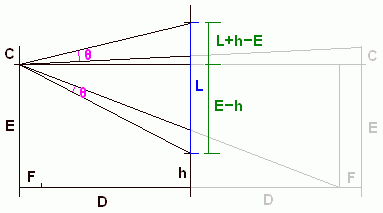
E is the height of your eyes.
C is the distance from your eyes to the top of your head. (C for crown.)
F is the distance your feet stick out from your eyes.
L is the length of the mirror.
D is the distance from you to the wall.
h is how high from the floor you should hang the mirror.
θ is the angle of the left over space above and below your reflection.
I used Quickmath again to solve the equation for h.
Here's an example solution using values for my mirror and body measurements.
E = 69 inC = 4 in
F = 7 in
L = 48 in
D = 36 in
h = 25.37997 in
θ = 3.757022°
Using the same values for E, C, F, and L, here are graphs that show how h and θ change as D increases. The previous model is shown in gray, the updated model is shown in red.
Links
Wikipedia Reference Desk
http://en.wikipedia.org/wiki/Wikipedia:Reference_desk
Volunteers answer reference desk-type questions.
Solving equation with inverse tangents
http://en.wikipedia.org/wiki/Wikipedia:Reference_desk/Archives/Mathematics/2008_March_25#Solving_equation_with_inverse_tangents
My post to the Wikipedia Mathematics Reference Desk where I got advice about how to solve the equation of this problem.
Quickmath
http://www.quickmath.com/
Automated solvers for equations, matrices, and other math problems.